Child's Play and Show your Work Fails

How long before Neolithic man did societies understand principles of geometry? I'm not going to look it up. It was long before Stonehenge was envisioned. It sparks the imagination doesn't it.

Imagine a stone age child playing with a wish bone shaped branch. One end of branch is poked into the ground and the other is rotated around in a manner which scribes a circle into the dirt. Now a kid without any technology what-so-ever, is going to think that is amazing. A parent is likely going to see demons and spirits. There are few circular items in the world and the dominant ones are the Sun and the Moon. Circles. They were very significant to early man. The local shaman would try to make sense of all of this and was probably one of the few people with the time to "experiment". It doesn't take much experimentation to come up with a hexagon using just a peg and a rope. Freaking magic is what it was.

Neolithic man knew how to create geometric plans without any mathematical skills. I'm sure simple counting was possible but not much more. With so little they designed and laid out Stonehenge. Thirty equally spaced orthostats aligned in a specific direction. So how come I had such a difficult time figuring it out. Just to prove I actually tried to figure it out I am doing what you had to do in school. Show your work!

My sort of first attempt. It was working but I didn't know what I was doing and I was measuring angles with a protractor for verification. After awhile I lost track and couldn't continue.

Cheating Fail!

Second attempt. Creating squares for intersection points. 32 resulting positions.

Square Fail!

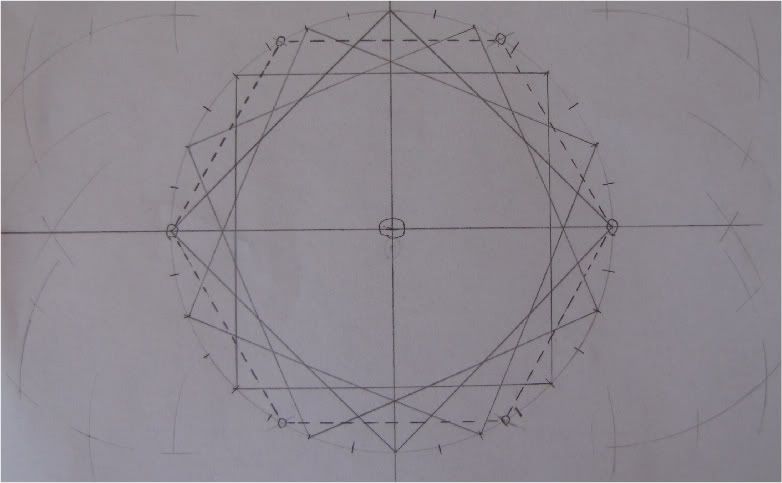
Third attempt. Used hexagons but started on the wrong vertex. Drew a cord between the wrong vertexes more than once and then lost track again.

Rotated hexagon Fail!

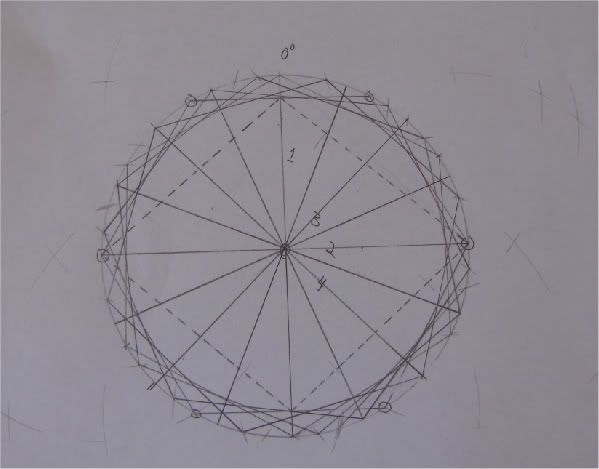
Fourth attempt. Setup the x,y axis as in previous attempts. Created intersections for the first hexagon. Properly aligned, this yields the first 6 orthostat intersection points. Now, I know I only have to do this four more times. An ancient surveyor would know he needed four equally spaced points between the ones already scribed. So he just keeps on using the radius of the circle to split the angles down until he has the equally spaced positions. I can't even describe it properly. If the ancient surveyor had something like a draftsman's dividers he could have taken some short cuts. No doubt he had to do it the way his father's, father's father's father did. Armed with tradition, rope and a peg and simple counting, 30 orthostat positions could be laid out in short order. Magic!

Hexagon win! The squares represent spaces and the circles are orthostat positions. I didn't bother to complete the exercise after I had to give up the lunch table.

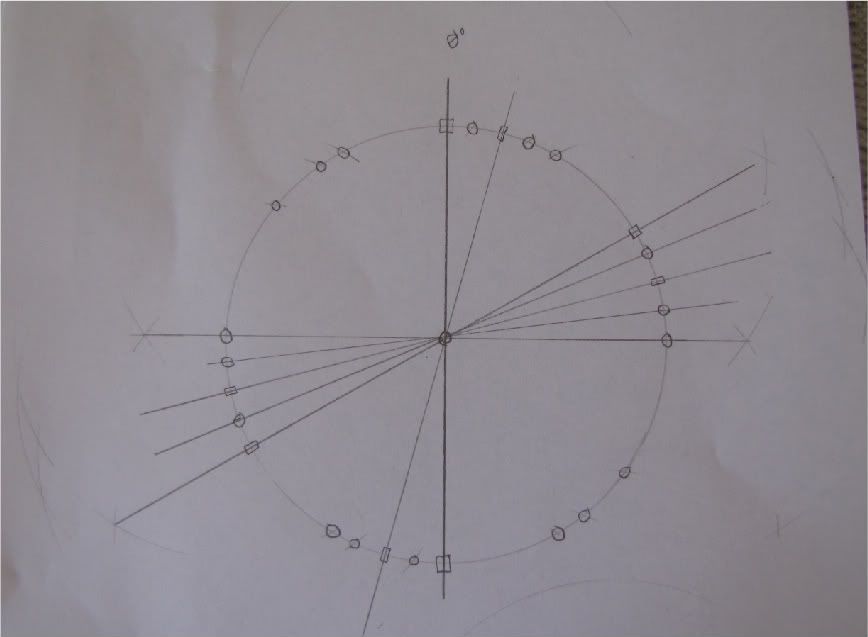
No pictures from REACH today but I have already moved the Great Trilithon by its own thickness and I am searching for a better vertex to re-establish two sets of the other Trilithons. I have experimented with the inner circle of stones called Bluestones. The only good block for them is the railing. A little narrow for my liking. Wider ones would give a better measure of cover and would simulate reality more accurately.